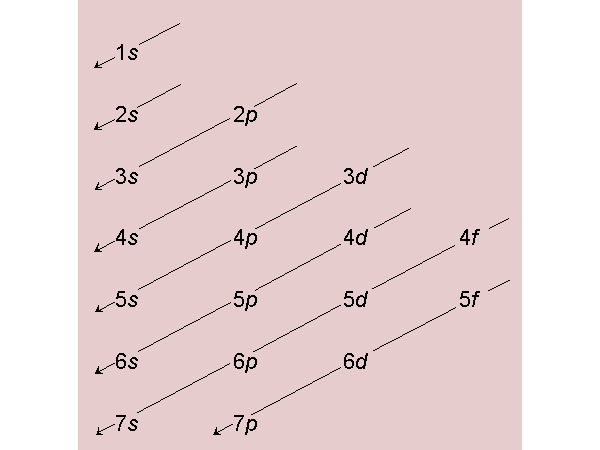Quantum Numbers and Electronic Structure

Quantum Numbers Table | Atomic Structure Slideshow  | Quantum Chemistry Quizzes 

To account for the behavior of an electron in an atom, it is not sufficient to describe the electron simply as a negatively charged particle; its wavelike properties must also be considered. The first such description of an electron came in 1926 with the development of Schrodinger's wave equation. The branch of science that deals with the solution of wave equations is called quantum mechanics (or wave mechanics). Each solution to a wave equation is characterized by three integers called quantum numbers. Each solution corresponds to a discrete energy and defines a region of space about the nucleus (called an orbital) where an electron having that energy is generally found. A fourth quantum number is also necessary for a unique description of an equation.

According to the quantum mechanical model, the allowed energy levels of an electron are composed of one or more orbitals, and the distribution of electrons about the nucleus is determined by the number and kinds of energy levels that are occupied. Therefore, in order to understand the way electrons are distributed, we must first examine the energy levels. This is best accomplished through a discussion of the four quantum numbers. The most important aspects of each quantum number are presented below.

The principal quantum number, n. The electronic energy levels in an atom are arranged roughly into principal levels (or shells) as specified by n. The value of n gives an indication of the position of an electron in the energy level relative to the nucleus; the larger the value of n, the greater the average distance of an electron from the nucleus and the higher its energy. The principal quantum number may have values as follows: n = 1, 2, 3, 4, …..

The azimuthal quantum number (also called subsidiary or secondary), l. Each principal energy level may be split into closely spaced sublevels (or sublevels) as specified by l. This quantum number may be more aptly named the orbital shape quantum number, since each orbital in a given type of sublevel (i.e., a given value of l) has the same "electron cloud" shape. For example, when l = 0, the orbital is spherical. For each principal energy level (designated by n) there are n sublevels (i.e., n values of l): l=0,1,2,3,…( n -1). Sublevels are commonly given letter designations. The l = 0,1,2,3,4,5, … sublevels are designated as s, p, d, f, g,…. sublevels, respectively. For known elements no value of l higher than 3 (f sublevel) is necessary.

Two quantum numbers (n and l) are required to specify a particular energy sublevel.

The magnetic quantum number, m_l. Each orbital within a particular sublevel is distinguished by its value of m_l. This quantum number may be more aptly named the orbital orientation quantum number. In each energy sublevel (designated by l) there are 2l+1 possible independent orientations of the electron cloud. Each orientation is defined by a value of ml and is called an orbital.

m_l = l, (l -1), (l -2), … 0 … -( l -2), -( l -1), -l or m_l = 0, ±1, ±2, ±3, … ±1

All orbitals in a given sublevel are of equal energy (they are degenerate). In the presence of a magnetic field their different orientations cause them to have different energies.

Three quantum numbers (n, l, and m_l) are required to specify a particular orbital.

The spin quantum number, m_s. An electron spins on its own axis as characterized by m_s. There are two possible directions of spin: m_s = +1/2 or -1/2. Since a spinning charge generates a magnetic field, an electron has a magnetic field associated with it. Two electrons in the same orbital are most stable when they have opposite spins (+1/2 and -1/2) due to a magnetic attraction. Such electrons are said to be paired electrons or each other's magnetic fields, but an unpaired electron may be detected by magnetic measurements. In fact, elements with unpaired electron are attracted by magnetic fields; such elements are called paramagnetic. Magnetic measurements have shown that electrons are distributed among the orbitals of a sublevel in a way that gives the maximum number of unpaired electrons with parallel spins (all m_s values have the same sign).

Four quantum numbers (n, l, m_l, and m_s) are required to specify a particular electron.

The following list is a condensation of some of the most useful information relevant to quantum numbers and electronic structure.

1. The four quantum numbers:
   • n = 1, 2, 3, …
   • l = 0, 1, 2, 3, …. (n-1)
   • m_l = 0, ±1, ±2, ±3, … ±l
   • m_s = +1/2 or -1/2

2. Sublevel Types
   

   QN l	Type	Orbitals	Total Electrons		QN l	Type	Orbitals	Total Electrons
   0	s	1	2		3	f	7	14
   1	p	3	6		4	g	9	18
   2	d	5	10		5	h	11	22

3. Principal energy level n contains: (a) n sublevels (b) n² orbitals (c) 2n² electrons maximum (see table above)
4. Sublevel l contains: (a) 2l+1 orbitals (b) 2(2l+1) electrons maximum
5. In the ground state electrons fill orbitals so that the total energy of the atom is minimized.
6. Sublevel energies increase as: (a) n increases: 1s<2s<3s…; 2p<3p<4p ….. etc. (b) l increases: 2s<2p; 3s<3p<3d; 4s<4p<4d<4f; etc.
7. Each orbital can hold a maximum of two electrons; they must be paired.
8. In a given sublevel electrons are distributed among the orbitals in a way that yields the maximum number of unpaired electrons with parallel spins.
9. For a given value of l, orbital shape remains the same. For example, orbitals with l = 0 (1s, 2s, 3s, etc. sublevels) are all spherical.
10. A given value of n designates a specific principal energy level. Given values of n and l designate a specific energy sublevel. Given values of n, l, and m_l designate a specific orbital. Given values of n, l, m_l, and m_s designate a specific electron.

To review the definitions and interrelationships of the 4 quantum numbers, study this Table. Careful study will show that the table is consistent with the statements listed above.

There are two common methods of indicating the arrangement of electrons in an atom. Unless otherwise stated, the lowest energy state (ground state) is given. These methods are electron configurations and atomic orbital diagrams.

An electron configuration shows the electrons distribution by sublevel using the quantum numbers n and l, where the notation for l is by its letter designation (s, p, d, f, etc.). For example, the notation 3d⁴ indicates 4 electrons in the d sublevel (l=2) of the n =3 principal energy level. You are referred to Chapter 7 in the textbook where a complete discussion of electron configuration may be found.

An atomic orbital diagram shows the electron distribution in an atom by means of a diagram which accounts for the distribution by all four quantum numbers.

1. An orbital is shown by a box, circle or line.
2. An electron is shown by an arrow.
3. The arrows also show the spin of the electron so that when two electrons are in the same orbital, the arrows point in opposite directions to represent their opposing spins.
4. Sublevels are shown by a designation under the appropriate orbitals (see examples below).

In the figure below, an atomic orbital diagram is used to illustrate the order of filling for the first ten electrons as shown by the numbers entered in the boxes. As an example, consider the electronic structure of sulfur.

Since sulfur has 16 electrons, its electron configuration is 1s² 2s² 2p⁶ 3s² 3p⁴

Atomic orbital diagram for sulfur with two unpaired electrons:

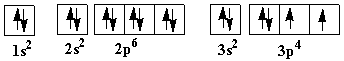The chart below shows the order of orbital fill up by electrons.  Remember that electrons ar put into the lowest available energy orbital before filling up a higher energy orbital.  In addition, you always put one electron in each of the degenerate orbitals of a particlar energy level before putting a second electron in any of the orbitals of the same energy (Hund's Rule).